Si hablamos de porcentajes a todos nos resulta un tema familiar, pero: ¿sabríamos decir qué es un porcentaje? ¿cómo se calcula?
El porcentaje es, realmente, un símbolo.
Un símbolo que representa una fracción de denominador 100. Así, en el lenguaje escrito, es mucho más sencillo escribir el porcentaje que la fracción:
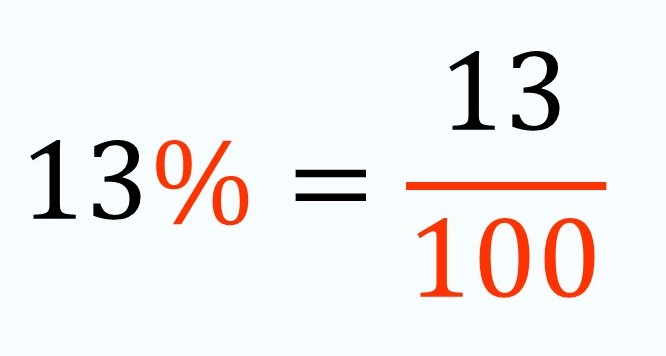
Este símbolo (%) se lee como “por ciento” e indica, como hemos dicho, el número de partes en que la unidad, o cantidad de referencia, ha sido dividida. Es decir, el porcentaje (%) siempre aparece en una expresión que relaciona dos cantidades. Por ejemplo: “El 13% de los niños que estudian en el I.E.S. Andrés Laguna eligen el batido de chocolate como su bebida favorita”. En este caso, las cantidades que se están relacionando son la cantidad de niños que estudian en nuestro instituto con la cantidad de esos niños que, además eligen el batido de chocolate como bebida favorita.













