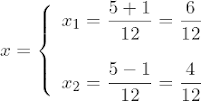martes, 11 de mayo de 2021
EL TEOREMA DE PITÁGORAS
Pinchando en la imagen se abrirá una nueva ventana con un documento que podrás imprimir, sobre Pitágoras y su teorema.
Puedes practicar este teorema con estos ejercicios que se esconden tras esta imagen:
PROBLEMAS CON ECUACIONES DE DOS INCÓGNITAS
Practica con problemas de ecuaciones de dos incógnitas (sistemas de ecuaciones). Pincha la imagen y podrás ver problemas sencillos con este tipo de ecuaciones. Intenta resolverlo y luego pincha en la solución para comprobarlo.
Pincha en la imagen para ver estos problemas.
martes, 4 de mayo de 2021
MOBY DICK SIN LÍMITES
Moby Dick sin límites busca sensibilizar a la sociedad sobre la igualdad de oportunidades de todas las personas a través de la cultura
Moby Dick sin límites
viernes, 30 de abril de 2021
RESOLUCIÓN DE SISTEMAS DE ECUACIONES
Cuando hablamos de buscar la solución a una ecuación con dos incógnitas, realmente lo que estamos buscando es la solución de un sistema de ecuaciones, es decir, el valor de 'x' y de 'y' (como ejemplo de dos incógnitas) en dos o más ecuaciones, siendo estos valores válidos para estas ecuaciones.
Por ejemplo, la solución de este sistema de ecuaciones:
2x + y = 16 x= 5
3y = 33 - 3x y= 6
(Para resolver estas dos ecuaciones, los únicos valores para 'x' e 'y' son '5' y '6' respectivamente. Esa es la solución).
Existen tres métodos para resolver este tipo de ecuaciones. Veamos cuales son con el ejemplo del sistema anterior de ecuaciones:
1.- Método de sustitución
Despejamos una incógnita de una de las ecuaciones y sustituimos su valor en la
otra ecuación.
Ejemplo:
a. Despejamos la 'y' en la primera ecuación:
y=16 - 2x
b. Sustituimos la 'y' de la segunda ecuación por el valor obtenido en la
primera ecuación:
3(16 - 2x) = 16 - 2x
c. Resolvemos la ecuación como una ecuación de una incógnita y
obtendremos el valor de 'x'. Posteriormente, en la primera ecuación
sustituimos la 'x' por el valor obtenido y obtendremos el valor de 'y'.
2.- Método de igualación
Despejamos una incógnita (la misma) de las dos ecuaciones e igualamos ambas
quedando como una ecuación de una incógnita.
Ejemplo:
a. Despejamos la 'y' en las dos ecuaciones:
y=16 - 2x
y= 33 - 3x
3
b. Puesto que en ambas hemos despejado 'y' colocamos los resultados a uno
y otro lado del signo =:
16 - 2x = 33 - 3x
3
c. Resolvemos la ecuación como una ecuación de una incógnita y
obtendremos el valor de 'x'. Posteriormente, en la primera ecuación
sustituimos la 'x' por el valor obtenido y obtendremos el valor de 'y'.
3.- Método de reducción
Se trata de "eliminar" una incógnia sumando las ecuaciones. Para ello,
multiplicamos todos los términos de una ecuación por un número que nos permita
"anular" una de las incógnitas.
Ejemplo:
a. Colocamos las ecuaciones, mediante transposición de términos, para que
coincidan los monomio:
2x + y = 16 ---------------------> 2x + y = 16
3y = 33 - 3x ---------------------> 3x + 3y = 33
b. Multiplicamos la primera ecuación por (-3). De esta forma, conseguiremos
"anular" la incógnita y al realizar la suma:
2x + y = 16 ----> x (-3) ----------------> -6x - 3 y = - 48
3x + 3y = 33 -------------------------------> 3x + 3y = 33
-3x = - 15
c. Resolvemos la ecuación como una ecuación de una incógnita y
obtendremos el valor de 'x'. Posteriormente, en la primera ecuación
sustituimos la 'x' por el valor obtenido y obtendremos el valor de 'y'.
En este vídeo podrás ver explicados estos tres métodos:
martes, 27 de abril de 2021
EL COMPLEMENTO PREDICATIVO Y EL COMPLEMENTO DE RÉGIMEN
EL COMPLEMENTO PREDICATIVO
Se trata de un tipo de complemento que tiene una doble función sintáctica: por un lado acompaña al verbo de la oración y por otro lado expresa una cualidad, propiedad o estado de un sustantivo, que puede ser el nucleo del sujeto o del complemento directo.
Mira estos ejemplos:
Su hija salió muy contenta del examen.
sujeto NV CPvo CCLugar
Encontré secas las flores.
NV CPvo CD
EL COMPLEMENTO DE RÉGIMEN
Podemos decir que el complemento de régimen se caracteriza porque el verbo al que acompaña siempre necesita de una preposición que le da sentido.
Por tanto, podemos definir el complemento de régimen como un sintagma preposicional cuya preposición es necesaria para que el verbo de la oración pueda tener significado.
Ejemplos:
En la primera oración, el verbo confundir siempre necesita una preposicón ("con") para que tenga sentido, ya que siempre confundimos alguna cosa con otra.
En el segundo caso, siempre advertimos de algo, de ahí que se necesite la preposición "de".
Mira este vídeo para comprenderlo mejor.
lunes, 26 de abril de 2021
ECUACIONES DE PRIMER GRADO CON DOS INCÓGNITAS
Aprende más en este vídeo:
jueves, 15 de abril de 2021
ECUACIONES DE 2º GRADO
Una ecuación
de segundo grado es toda expresión de la forma:
Donde a, b y c son las constantes de
la ecuación:
·
a es
el número que va siempre delante de x al cuadrado.
·
b es
el número que va siempre delante de la x.
·
c es
el número.
Debemos
tener en cuenta que las ecuaciones de 2º grado siempre tienen dos
soluciones.
RESOLUCIÓN DE ECUACIONES DE 2º GRADO
Se pueden
dar varios casos:
CASO 1: Ecuaciones completas
La ecuación tiene todos los elementos
La
ecuación de segundo grado se resuelve aplicando la siguiente fórmula:
1 Primero encontramos
los valores de los coeficientes
2 Sustituimos los
valores en la fórmula y resolvemos
3 Observamos que se obtienen dos valores para X, estos usualmente se representan por
4 Simplificamos los
resultados y obtenemos
CASO 2: Ecuaciones incompletas
La ecuación no tiene todos los elementos.
Dependiendo de los elementos que falte, el modo de resolución varía. Veamos
algunos ejemplos:
Ejemplo a:
x2=k
La resolución es simple: se trata de despejar la x, y hallar
la raíz cuadrada de k.
Por ejemplo:
X2=36
El resultado será la raiz cuadrada de 36. Recuerda que la raíz cuadrada tiene una solución positiva y otra negativa:
x= +6
x= -6
Ejemplo b:
Por ejemplo:
Para resolver ecuaciones de
segundo grado incompletas de este tipo, en primer lugar despejamos
x² como si fuera una ecuación de primer grado:
Una vez aquí, tenemos que
pasar el cuadrado al otro lado de la igualdad en forma de raíz, para después
obtener una solución positiva y otra negativa:
CASO 3:
Por ejemplo:
El primer paso para resolver
este tipo de ecuaciones incompletas es sacar factor común, ya que una x se repite en los dos términos.
Tenemos que dar otro paso más,
que es despejar la x:
Las soluciones 0 y 3